1 简介
本文介绍的工作已经发表在Knowledge-based systems,英文标题为A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs。
多旅行商问题(multiple traveling salesman problems,MTSP)是指给定m个旅行商以及n个城市的坐标或者相对距离,m个旅行商分别获取需要旅行的城市,并各自规划合理的遍历路径,使得每一个城市被一个旅行商且只被一个旅行商访问一次。MTSP的目标函数通常是最小化所有旅行商遍历路径长度的总和,或者最小化m个旅行商路径中最长路径。MTSP来源于实际应用,例如交通运输、物流配送、灾后救援等,同时MTSP又是经典组合优化问题之一。适用于MTSP问题的高效求解方法或可推动实际应用以及其他组合优化问题的深入研究。然而,MTSP由于解空间过大,整数规划和启发式算法在这一问题上的计算复杂度都极高。深度学习领域对MTSP的研究成果也十分有限,主要困难体现在:1)MTSP的搜索 空间随着Agent和任务节点数量的增加急剧增长;2)MTSP是NP-hard问题,计算 复杂度极高,因此缺乏具有最优解的训练集和测试集;3)MTSP是一个协同型任务,需 要多个Agent合作才能得到近似最优解,因此设计一种新的可以提取Agent之 间协作关系的模型至关重要。
文章设计了一个由共享图神经网络和分布式策略组成的网络模型来学习适用于MTSP的共有策略表达。图网络(graph neural network)用来抓取MTSP工作图上的重要信息,策略网络 (policy network)计算子任务相对于Agent的重要性。网络模型采用 S样本批训练强化学习方法帮助学习高效的策略表达,同时克服了由于计算复杂度极高导致的训练集缺乏问题。通过网络模型学到的策略表达方式,可以将大规模的MTSP划分为m个小规模的TSP,现有的其他算法或工具可快速求解小规模TSP。通过这种方式,极大的压缩了 MTSP的搜索空间。最后,文章还通过大量的实验验证了任务协同模型明显优于其他算法和模型,并且S样本批训练强化学习也确实提升了模型的学习效果。
2 神经网络模型设计
MTSP是作用在图上的经典问题,为学到有效策略,首先每一个Agent应该解析全局工作图的状态信息,然后各Agent协同决策出每一个Agent访问的节点集。通过这种方式,含有多子任务的MTSP问题可划分为m个小规模TSP,而小规模TSP 的近似最优解可以通过许多有效的算法和工具快速求解。
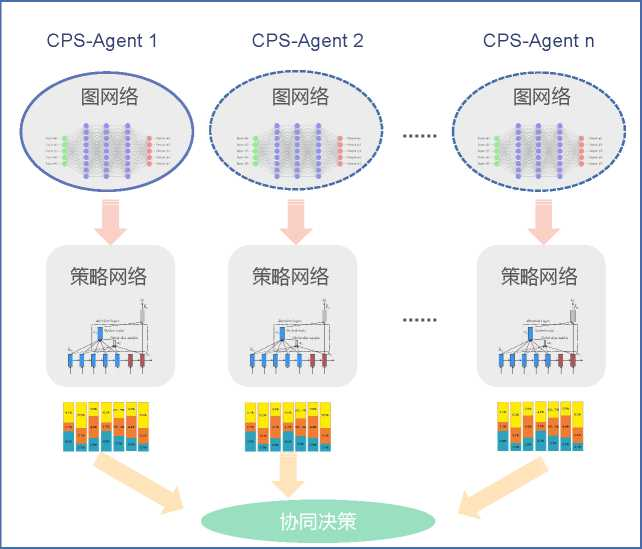
图1: 适用于MTSP策略学习的神经网络模型结构
文章设计的总体神经网络模型如图1所示。图中,每一个Agent的网络结模型分为两部分:图网络(graph neural network)和策略网络(policy network)。图网络抓取MTSP工作图上的重要信息,策略网络计算节点相对于Agent的重要性。所有 Agent的图网络结构和参数均完全相同,策略网络则各自独立。Agent最终根据各自计算的节点重要性协同决策。
2.1 图神经网络模型
首先简要说明 CMPNN (compositional message-passing neural network)的框架设计。 CMPNN根据图中节点之间的连接关系,在相邻节点之间消息传递,最终为图中的每一 个节点v∈V计算出p-维的特征向量计算出。具体来说,CMPNN是MPNN (messagepassing neural network) 的升级版。MPNN是从之前的图嵌入技术总结的共有框架,框架结 构包含四部分:消息制造、消息收集、消息传递、图嵌入,如式(3-1),其中, 表示节点u的邻居节点集合,M和Ψ是神经网络模型,ф和h是激活函数。
表示节点u的邻居节点集合,M和Ψ是神经网络模型,ф和h是激活函数。
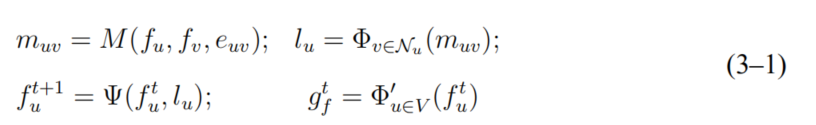
CMPNN采用了额外的神经网络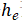 预测边的重要性。然后通过引入一个全局不变的内核
预测边的重要性。然后通过引入一个全局不变的内核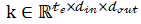 ,CMPNN每一次迭代的计算过程如式(3-2)所示。式(3-2)的节点特征更新过程与图的结构相关。多轮节点特征更新可以使得消息传递的更远,也就是说,如果图网络在T次迭代后停止,则节点特征
,CMPNN每一次迭代的计算过程如式(3-2)所示。式(3-2)的节点特征更新过程与图的结构相关。多轮节点特征更新可以使得消息传递的更远,也就是说,如果图网络在T次迭代后停止,则节点特征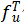 包含来自T-hop的邻居的信息。
包含来自T-hop的邻居的信息。

接下来讨论本章在CMPNN框架下参数化神经网络模型的问题。具体来说,本章将 节点的特征更新过程形式化表示为式(3-3)。式中,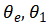 和
和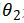 是神经网络模型参数,
是神经网络模型参数,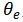 是所有边共享的网络参数,
是所有边共享的网络参数,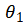 和
和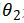 是所有节点共享的参数,relu是作用在输入元素的线性整流函数
是所有节点共享的参数,relu是作用在输入元素的线性整流函数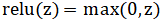 。作用在所有邻居的 max是整合邻居信息的聚合函数。 T次迭代后得到的节点特征和图嵌入可以提供给分布式策略网络重要信息。
。作用在所有邻居的 max是整合邻居信息的聚合函数。 T次迭代后得到的节点特征和图嵌入可以提供给分布式策略网络重要信息。
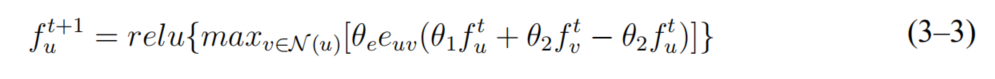
2.2 分布式策略网络
分布式策略网络对应于每一个Agent,即m个Agent的MTSP对应的分 布式策略网络包含m个子网络。分布式策略网络计算过程分为两个阶段。第一阶段: Agent特征向量构造,即每个Agent通过全局图嵌入和节点特征,独立构造自 己的特征向量。第二阶段:策略分配,即每一个Agent根据自身特征向量和全局图 嵌入计算每一节点相对于自身的重要性,然后所有Agent根据节点重要性依概率确 定自身子任务集。依概率分配使得网络模型可以采用策略梯度(policy gradient)训练。
文章在Agent特征向量构造和策略分配两部分均采用了 “注意力机制(attention mechanism)”。目前已经有许多受欢迎的注意力机制被提出,包括content-based attention, dot-product, general attention,等等。分布式策略网络允许每个 Agent 采用不同的策略学习机制。文章的实验中,分布式策略网络的m个子网络均采用相同的 结构,只是神经元参数不同。详细计算过程请参考原文。
2.3 S-样本批训练强化学习
为评估模型参数θ,文章最大化策略的期望收益
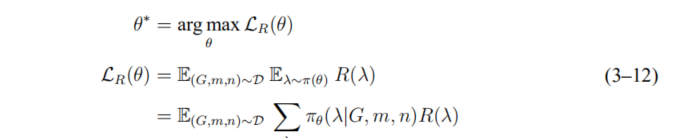
其中,D是训练集;λ是一次依策略分配;R(λ)是依策略λ分配的收益;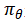 是在当前模型参数θ作用下的策略分配的分布,即
是在当前模型参数θ作用下的策略分配的分布,即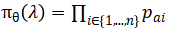 。
。
但是,在式(3-12)中,对所有分配求和是非常难以计算的。为克服这一难点,学术 界通常引入one-sample近似,即通过依策略采样一次,然后计算该采样的收益,用该收 益近似这一策略的总体收益。但是这样的近似方法在梯度评估时引入了明显的误差,为减小误差并加速收敛,本章采用了 S-样本近似,即
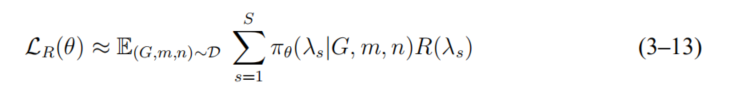
为进一步减小训练误差,本章还引入优势函数(advantage function),将优势函数和损失函数相结合,可得到最终的优化函数为:

实验中所有策略分配的收益均由OR-Tools计算。OR-Tools可以快速求解小规模TSP, 并且返回最长旅行距离的相反数作为本次分配的收益。
采用S-样本近似的主要优点包括:1)对策略评估的更加准确;2)降低了训练误差; 3)加快了学习速度。
3 实验设计及分析
为论证文章提出的模型GNN+DisPN有能力为MTSP学到高效的求解策略,首先, 本章选择在于训练集规模相同的测试集上做一般性检验,将GNN+DisPN与精确解求解 器Gurobi.元启发算法求解工具OR-Tools的计算结果比较,实验结果统计如表1所示;然后,在规模远超于训练 集的测试集上做泛化测试,将小规模MTSP上学到的策略直接应用到大规模问题中,实验结果如表2所示。具体实验结果可参考原文。总体来说,文章提出的方法实现了MTSP的快速高效求解,并且模型可泛化至大规模的MTSP中,文章的测试案例最多包含10个Agent,1000个节点。
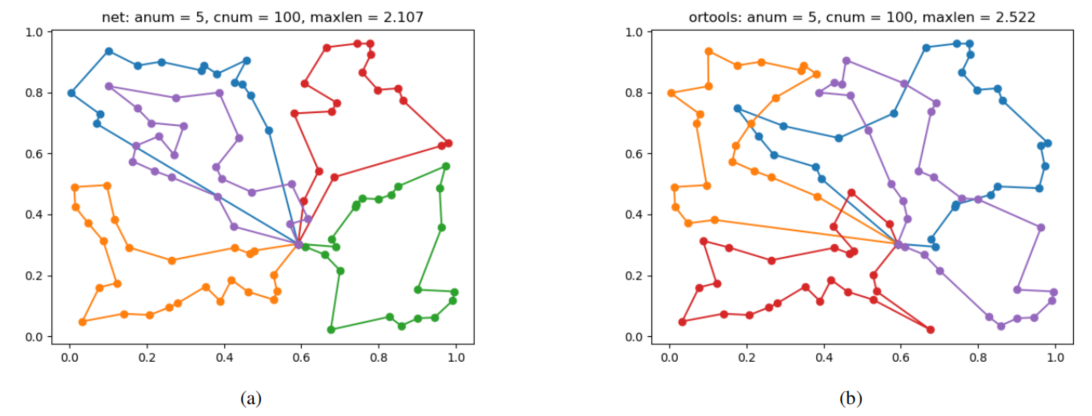
图1:MTSP的实验结果可视化显示
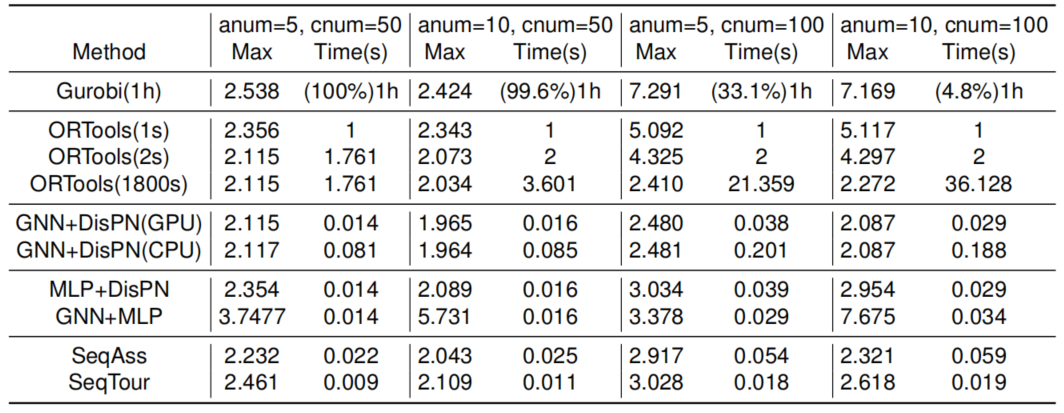
表 1: 在同一规模的MTSP上训练和测试的实验结果统计

表 2:小规模MTSP数据集上训练的网络模型泛化结果统计
文章还通过两个案例可视化展示了多种方法下MTSP的规划结果,例如图2所示的案例可视化展示了本文提出的方法以及OR-Tools规划的实验结果。最后通过实验论证了S-样本池强化学习对策略学习的积极促进作用,如图3所示。
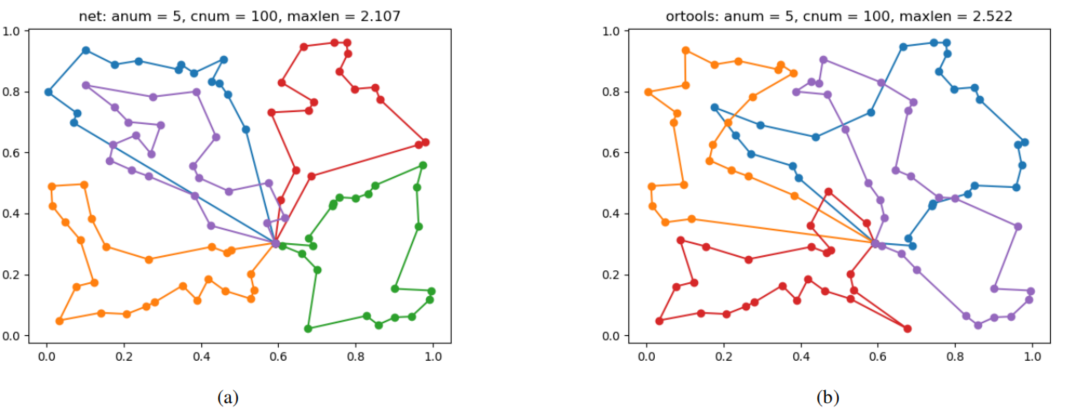
图2: 包含5个Agent 100 个城市的MTSP采用本文提出的方法以及OR-Tools规划的结果可视化展示
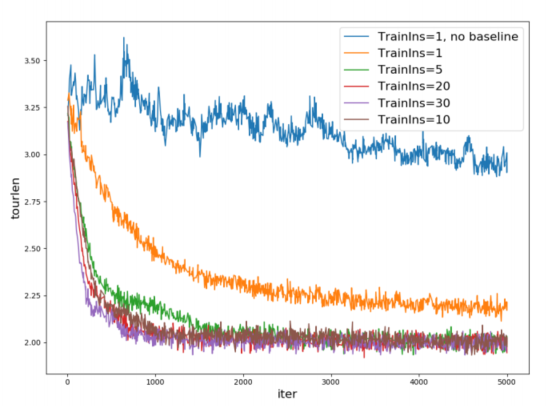
图3: S-样本池强化学习对策略学习的促进作用
该成果由胡玉姣(西北工业大学在读博士生)、姚远(西北工业大学副教授)、Lee Wee Sun(新加坡国立大学教授)合作完成,“A Reinforcement Learning Approach for Optimizing Multiple Traveling Salesman Problems over Graphs”发表在Knowledge-based Systems(中科院一区期刊)